The following comes from William Noyes’s 1910 classic, Handwork in Wood. See our previous Handwork in Wood posts here.
B. Tools for holding other tools: Wood Braces
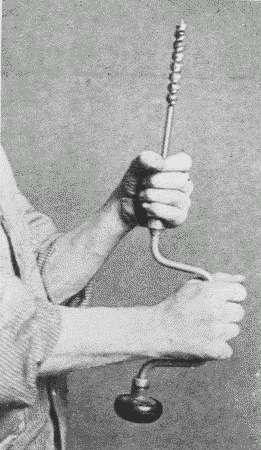
The brace or bit-stock, Fig. 185, holds all sorts of boring tools as well as screwdrivers, dowel-pointers, etc. The simple brace or bit-stock consists of a chuck, a handle, and a knob, and is sufficient for ordinary use; but the ratchet-brace enables the user to bore near to surfaces or corners where a complete sweep cannot be made. It is also useful where sufficient power can be applied only at one part of the sweep. By means of pawls which engage in the ratchet-wheel, the bit can be turned in either direction at the will of the user. The size of the brace is indicated by the “sweep,” that is, the diameter of the circle thru which the swinging handle turns. To insert a bit or other tool, Fig. 186, grasp firmly with one hand the sleeve of the chuck pointing it upward, and revolve the handle with the other hand, unscrewing the sleeve until the jaws open enough to admit the whole tang of the bit. Then reverse the motion and the bit will be held tightly in place. Various hand-, breast-, bench-, bow-drills and automatic drills are of use in doing quick work and for boring small holes, Fig. 187.
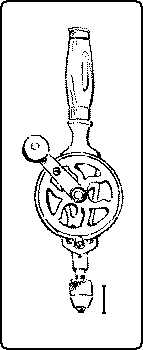
Fig. 187. Hand-Drill.
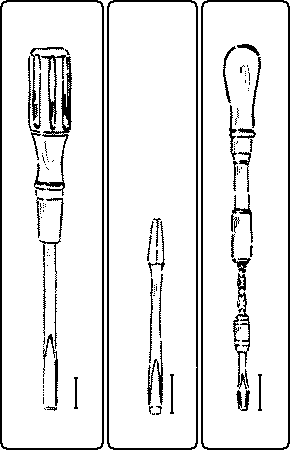
The screwdriver, Fig. 188, is a sort of holding tool for turning, and so driving screws. Various devices have been tried to prevent the twisting in the handle. This is now practically assured in various makes. The other important matter in a screwdriver is that the point be of the right temper, so as neither to bend nor to break. If the corners break they can be reground, but care should be taken not to make the angle too obtuse or the driver will slip out of the slot in the screw-head. The bevel should have a long taper. A shop should be equipped with different sizes of screwdrivers to fit the different sizes of screws. Screwdrivers vary in size, the shank ranging in length from 2½” to 18″. A long screwdriver is more powerful than a short one, for the screwdriver is rarely exactly in line with the axis of the screw, but the handle revolves in a circle. This means an increased leverage, so that the longer the screwdriver, the greater the leverage.
| 188 | 189 | 190 |
| Fig. 188. Screwdriver. Fig. 189. Screwdriver-Bit. Fig. 190. Spiral Screwdriver. |
For heavy work, screwdriver-bits, Fig. 189, in a bit-stock are useful, and for quick work, the spiral screwdriver, Fig. 190, and for small work, the ratchet-screwdriver.
7. MEASURING AND MARKING TOOLS.
It is a long step from the time when one inch meant the width of the thumb, and one foot meant the length of the foot, to the measuring of distances and of angles which vary almost infinitesimally. No such accuracy is necessary in measuring wood as in measuring metal, but still there is a considerable variety of tools for this purpose.
For measuring distances, the rule, Fig. 191, is the one in most common use. It is usually made of boxwood. For convenience it is hinged so as to fold. A rule is called “two-fold” when it is made of two pieces, “four-fold” when made of four pieces, etc. When measuring or marking from it, it can be used more accurately by turning it on edge, so that the lines of the graduations may come directly against the work. The one in most common use in school shops, is a two-foot, two-fold rule. Some instructors prefer to have pupils use a four-fold rule, because that is the form commonly used in the woodworking trades. Steel bench-rules, Fig. 192, are satisfactory in school work because unbreakable and because they do not disappear so rapidly as pocket rules. They need to be burnished occasionally.
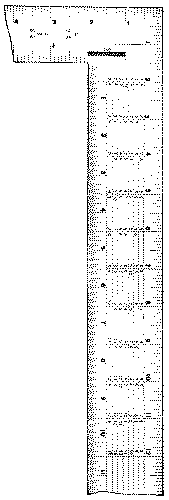
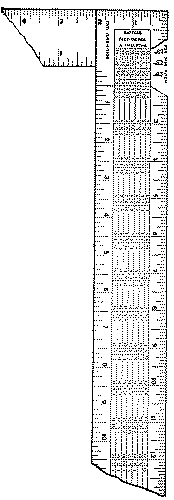
The steel square, Figs. 193, 194, 196, 197, is useful, not only as a straight-edge and try-square, but also for a number of graduations and tables which are stamped on it. There are various forms, but the one in most common use consists of a blade or “body” 24″ × 2″ and a “tongue,” 16″ × 1½”, at right angles to each other. Sargent’s trade number for this form is 100. It includes graduations in hundredths, thirty-seconds, sixteenths, twelfths, tenths, and eighths of an inch, also a brace-measure, an eight-square measure, and the Essex board-measure. Another style, instead of an Essex board-measure, and the hundredths graduation has a rafter-table. The side upon which the name of the maker is stamped, is called the “face,” and the reverse side the “back.”
The brace-measure is to be found along the center of the back of the tongue, Fig. 193. It is used thus: the two equal numbers set one above the other represent the sides of a square, and the single number to their right, represents in inches and decimals, the diagonal of that square.
| E. g., | 54 | 76.37 means that a square the sides of which are 54″ would have a diagonal of 76.37″. |
| 54 |
For determining the length of the long side (hypothenuse) of a right angle triangle, when the other two given sides are not equal, the foot rule, or another steel square may be laid diagonally across the blade and arm, and applied directly to the proper graduations thereon, and the distance between them measured on the rule. If the distance to be measured is in feet, use the 1⁄12″ graduations on the back of the square.
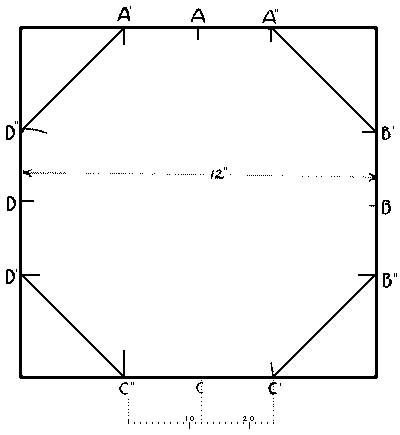
To use the octagonal (or 8-square) scale, Fig. 194, which is along the center of the face of the tongue, with the dividers, take the number of spaces in the scale to correspond with the number of inches the piece of wood is square, and lay this distance off from the center point, on each edge of the board. Connect the points thus obtained, diagonally across the corners, and a nearly exact octagon will be had. E.g., on a board 12″ square, Fig. 195, find A.B.C.D., the centers of each edge. Now with the dividers take 12 spaces from the 8-square scale. Lay off this distance on each side as A’ A” from A, B’ B” from B, etc. Now connect A” with B’, B” with C’, C” with D’, D” with A’, and the octagon is obtained.
In making a square piece of timber octagonal, the same method is used on the butt, sawed true. When the distance from one center is laid off, the marking-gage may be set to the distance from the point thus obtained to the corner of the timber, and the piece gaged from all four corners both ways. Cutting off the outside arrises to the gaged lines leaves an octagonal stick.
The board-measure is stamped on the back of the blade of the square, Fig. 196. The figure 12 on the outer edge of the blade is the starting point for all calculations. It represents a 1″ board, 12″ wide, and the smaller figures under it indicate the length of boards in feet. Thus a board 12″ wide, and 8′ long measures 8 square feet and so on down the column. To use it, for boards other than 12″ wide:—find the length of the board in feet, under the 12″ marked on the outer edge of the blade, then run right or left along that line to the width of the board in inches. The number under the width in inches on the line showing the length in feet, gives the board feet for lumber 1″ thick.
For example, to measure a board 14′ long, and 11″ wide,—under the figure 12, find 14 (length of the board); to the left of this, under 11 is the number 12.10; 12′ 10″ is the board-measure of the board in question. Since a board 12′ long would have as many board feet in it as it is inches wide, the B. M. is omitted for 12′ boards. Likewise a board 6′ long would have ½ the number of board feet that it is inches wide. If the board is shorter than the lowest figure given (8) it can be found by dividing its double by 2.; e. g., to measure a board 5′ long and 9″ wide, take 10 under the 12, run to the left of the number under 9, which is 7′ 6″; ½ of this would be 3′ 9″, the number of board feet in the board.
If the board to be measured is longer than any figure given, divide the length into two parts and add the result of the two parts obtained separately. For example, for a board 23′ long and 13″ wide,—take 12’ × 13″ =13′; add to it, 11’ × 13″=11′ 11″; total, 24’11”.
A good general rule is to think first whether or not the problem can be done in one’s head without the assistance of the square.
The table is made, as its name, Board-Measure (B. M.) implies, for measuring boards, which are commonly 1″ thick. For materials more than 1″ thick, multiply the B. M. of one surface by the number of inches thick the piece measures.
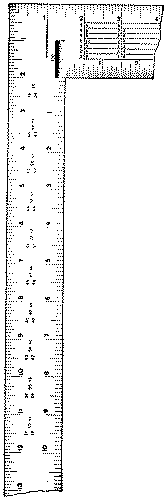
The rafter-table is found on the back of the body of the square, Fig. 197. Auxiliary to it are the twelfth inch graduations, on the outside edges, which may represent either feet or inches.
By the “run” of the rafter is meant the horizontal distance when it is set in place from the end of its foot to a plumb line from the ridge end, i. e., one half the length of the building, Fig. 198. By the “rise” of the rafter is meant the perpendicular distance from the ridge end to the level of the foot of the rafter. By the pitch is meant the ratio of the rise to twice the run, i. e., to the total width of the building. In a ½ pitch, the rise equals the run, or ½ the width of the building; in a ⅓ pitch the rise is ⅓ the width of the building; in a ¾ pitch the rise is ¾ the width of the building.
To find the length of a rafter by the use of the table, first find the required pitch, at the left end of the table. Opposite this and under the graduation on the edge representing the run in feet, will be found the length of the rafter; e.g., a rafter having a run of 12′ with a ¼ pitch, is 13′ 5″ long, one with a run of 11′ and a ⅓ pitch, is 13′ 28⁄12″, one with a run of 7′ and a ⅝ pitch, is 11′ 26⁄12″ long, etc.
When the run is in inches, the readings are for 1⁄12 of the run in feet: e.g., a rafter with a run of 12″ and a ¼ pitch is 135⁄12″, one with a run of 11″ and a ⅓ pitch, is 133⁄12″. Where the run is in both feet and inches, find the feet and the inches separately; and add together; e.g., a rafter with a run of 11′ 6″, and a ½ pitch, is 15′ 68⁄12″ + 86⁄12″ = 16′ 32⁄12″.
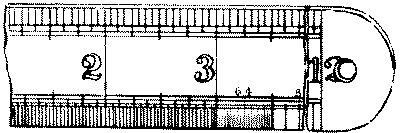
The lumberman’s board-rule, Fig. 199. To measure wood by it, note the length of the board in feet at the end of the measure. The dot nearest the width (measured in inches) gives the B. M. for lumber 1″ thick.
The try-square, Fig. 200, which is most commonly used for measuring the accuracy of right angles, is also convenient for testing the width of a board at various places along its length, for making short measurements, and as a guide in laying out lines with a pencil or knife at right angles to a surface or edge. The sizes are various and are indicated by the length of the blade. A convenient size for the individual bench and for ordinary use has a blade 6″ long. It is also well to have in the shop one large one with a 12″ blade.
| Fig. 200. Try-Square. | Fig. 201. Miter-Square. | Fig. 202. Sliding-T Bevel. |
In testing the squareness of work with the try-square, care must be taken to see that the head rests firmly against the surface from which the test is made, and then slipped down till the blade touches the edge being tested, Fig. 203. The edge should be tested at a number of places in the same way: that is, it should not be slid along the piece. The try-square is also of great use in scribing lines across boards, Fig. 204. A good method is to put the point of the knife at the beginning of the desired line, slide the square, along until it touches the knife-edge; then, resting the head of the square firmly against the edge, draw the knife along, pressing it lightly against the blade, holding it perpendicularly. To prevent the knife from running away from the blade of the try-square, turn its edge slightly towards the blade.
The miter-square, Fig. 201, is a try-square fixed at an angle of 45°.
The sliding T bevel, Fig. 202, has a blade adjustable to any angle. It may be set either from a sample line, drawn on the wood, from a given line on a protractor, from drawing triangles, from the graduations on a framing square, or in other ways. It is used similarly to the T-square.
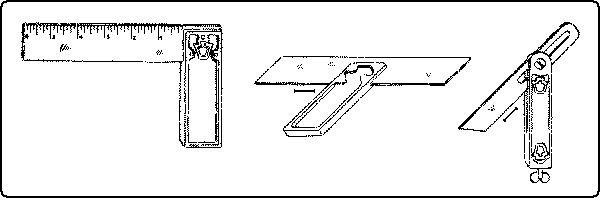
| Fig. 200. Try-Square. | Fig. 201. Miter-Square. | Fig. 202. Sliding-T Bevel. |
Noyes, W. (1910). Chapter IV. WOOD HAND TOOLS. In Handwork in Wood (pp. 95-104). Peoria, Ill.: Manual Arts Press
Learn all about woodworking and more online here at the Heritage School of Woodworking’s Online Woodworking Courses. See our Basics of Joinery Course for all about how measuring tools are used. To learn how to make your own tools, including measuring ones, see our Toolmaking Class.






Comments are closed.